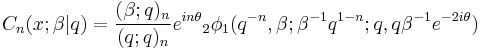Rogers polynomials
Not to be confused with Rogers–Szegő polynomials.
In mathematics, the Rogers polynomials, also called Rogers–Askey–Ismail polynomials and continuous q-ultraspherical polynomials, are a family of orthogonal polynomials introduced by Rogers (1892, 1893, 1894) in the course of his work on the Rogers–Ramanujan identities. They are q-analogs of ultraspherical polynomials, and are the Macdonald polynomials for the special case of the A1 affine root system (Macdonald 2003, p.156).
Askey & Ismail (1983) and Gasper & Rahman (2004, 7.4) discuss the properties of Rogers polynomials in detail.
Definition
The Rogers polynomials can be defined in terms of the descending Pochhammer symbol and the basic hypergeometric series by
where x = cos(θ).
References
- Askey, Richard; Ismail, Mourad E. H. (1983), "A generalization of ultraspherical polynomials", in Erdős, Paul, Studies in pure mathematics. To the memory of Paul Turán., Basel, Boston, Berlin: Birkhäuser, pp. 55–78, ISBN 978-3-7643-1288-6 978-3-7643-1288-6, MR820210, http://books.google.com/books?id=WePuAAAAMAAJ
- Gasper, George; Rahman, Mizan (2004), Basic hypergeometric series, Encyclopedia of Mathematics and its Applications, 96 (2nd ed.), Cambridge University Press, doi:10.2277/0521833574, ISBN 978-0-521-83357-8, MR2128719
- Macdonald, I. G. (2003), Affine Hecke algebras and orthogonal polynomials, Cambridge Tracts in Mathematics, 157, Cambridge University Press, doi:10.1017/CBO9780511542824, ISBN 978-0-521-82472-9, MR1976581
- Rogers, L. J. (1892), "On the expansion of some infinite products", Proc. London Math. Soc. 24 (1): 337–352, doi:10.1112/plms/s1-24.1.337, JFM 25.0432.01
- Rogers, L. J. (1893), "Second Memoir on the Expansion of certain Infinite Products", Proc. London Math. Soc. 25 (1): 318–343, doi:10.1112/plms/s1-25.1.318
- Rogers, L. J. (1894), "Third Memoir on the Expansion of certain Infinite Products", Proc. London Math. Soc. 26 (1): 15–32, doi:10.1112/plms/s1-26.1.15